Corona SDK – Curve fitting 1 – Implementation of Ramer-Douglas-Peucker algorithm to reduce points of a curve

This article is the first part of a two part tutorial to do curve fitting. The motivation to do this came when I was playing the Flight Control Center game on my IPhone. I was very interested in this kind of game and wanted to know how to build a game like that. I wrote a sample on Corona SDK but the result was not as I expected. I found the airplane oscillated like a doll 🙂 Soon, I recognized the reason: because the path I had made was not smooth. Moreover, I recognized that to draw a smooth curve on a touched screen is almost impossible. So my mission was quite clear: “drawing a smooth curve that approximately like the curve made”.
I looked on the Internet for the solution and came up with the combination of 2 algorithms for curve fitting that solve the issue beautifully. Basically, there are two steps to be implemented:
– First, reduce the points of the handmade curve by approximating it using the algorithm of Ramer-Douglas-Peucker. This article is all about the implementation of this on LUA language for Corona SDK. I won’t write too much about the algorithm’s explanation as it was done greatly in the wiki.
– Second, draw a continuous curve through the received points in step 1 using the algorithm of P.J.Schneider. The implementation of this is also on Corona and comes on the next post.
Let’s have a look on the pseudo code provided from the wiki:

function DouglasPeucker(PointList[], epsilon)
    // Find the point with the maximum distance
    dmax = 0
    index = 0
    for i = 2 to (length(PointList) - 1)
        d = PerpendicularDistance(PointList[i], Line(PointList[1], PointList[end])) 
        if d > dmax
            index = i
            dmax = d

    // If max distance is greater than epsilon, recursively simplify
    if dmax >= epsilon
        // Recursive call
        recResults1[] = DouglasPeucker(PointList[1...index], epsilon)
        recResults2[] = DouglasPeucker(PointList[index...end], epsilon)

        // Build the result list
        ResultList[] = {recResults1[1...end-1] recResults2[1...end]}
    else
        ResultList[] = {PointList[1], PointList[end]}

    // Return the result
    return ResultList[]
end

The PerpendicularDistance mentioned in the pseudo code is the distance from a point to a line that is measured by the length of the line that perpendicularly connects that point to the line. It is more explained by the below figure:

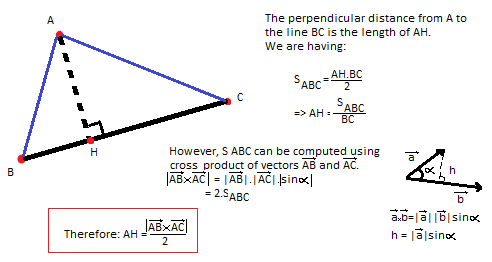
The LUA code for calculating perpendicular distance:

-- calculating the distance from point1 to the line goes through point2 and point3
-- cross product of two vectors: v1 = (point1, point2) and v2 = (point1, point3)
-- ==> v1(x, y) = (point2.x - point1.x, point2.y - point1. y); v2(x, y) = (point3.x - point1.x, point3.y - point1. y)
-- v1 x v2 = v1.x.v2.y - v1.y.v2.x
function dPointLine(point1, point2, point3)
    -- calculates area of the triangle
    local area = math.abs(0.5 * (point2.x * point3.y + point3.x * 
    point1.y + point1.x * point2.y - point3.x * point2.y - point1.x * 
    point3.y - point2.x * point1.y))
    -- calculates the length of the bottom edge
    local bottom = math.sqrt((point2.x - point3.x) ^ 2 + (point2.y - point3.y) ^ 2)
    -- the triangle's height is also the distance found
    local height = area / bottom

    return height
end

Here’s the code for implementing the main algorithm, please refer to the above pseudo code

-- points are the set of points to be reduced
-- tolerance is value indicates degree of correctness for approximation
-- the other parameters are for recursion
function douglaspeucker(points, firstpoint, lastpoint, tolerance, pointIndices)
	local maxD = 0
	local indexFurthest = 0

	for i = firstpoint, lastpoint do
		local distance = dPointLine(points[i], points[firstpoint], points[lastpoint])

		if distance > maxD then
			maxD = distance
			indexFurthest = i
		end
	end

	if maxD > tolerance and indexFurthest ~= 1 then
		table.insert(pointIndices, indexFurthest)

		douglaspeucker(points, firstpoint, indexFurthest, tolerance, pointIndices)
		douglaspeucker(points, indexFurthest, lastpoint, tolerance, pointIndices)
	end
end

And here’s the full source code. Enjoy 🙂

Advertisement